סיכום התכונות המכניות של חומרי מתכת

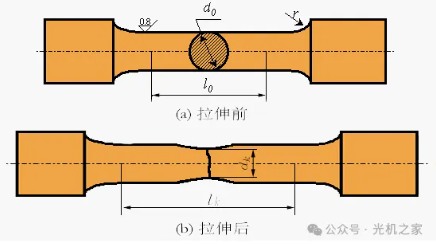
מבחן חוזק מתיחה משמש בעיקר לקביעת יכולתם של חומרי מתכת לעמוד בפני נזק במהלך תהליך המתיחה, והוא אחד המדדים החשובים להערכת התכונות המכניות של חומרים.

1. בדיקת מתיחה

בדיקת המתיחה מבוססת על עקרונות בסיסיים של מכניקת החומר. על ידי הפעלת עומס מתיחה על דגימת החומר בתנאים מסוימים, הדבר גורם לעיוות מתיחה עד שהדגימה נשברת. במהלך הבדיקה, נרשמים העיוות של הדגימה הניסיונית תחת עומסים שונים והעומס המקסימלי כאשר הדגימה נשברת, על מנת לחשב את חוזק הכניעה, חוזק המתיחה ומדדי ביצועים אחרים של החומר.

מאמץ σ = F/A

σ הוא חוזק המתיחה (MPa)

F הוא עומס המתיחה (N)

A הוא שטח החתך של הדגימה

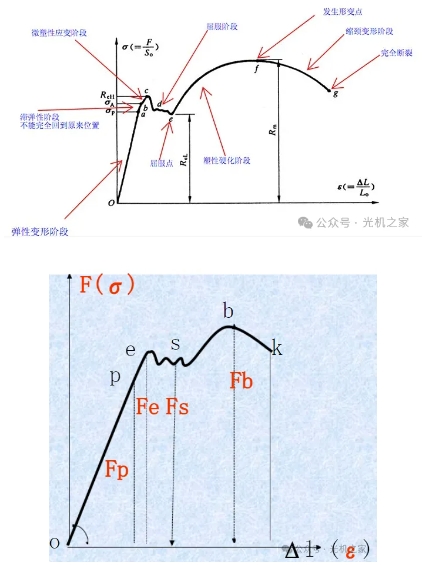
2. עקומת מתיחה

ניתוח של מספר שלבים בתהליך המתיחה:

א. בשלב OP עם עומס קטן, ההתארכות נמצאת ביחס ליניארי עם העומס, ו-Fp הוא העומס המקסימלי לשמירה על קו ישר.

ב. לאחר שהעומס עולה על Fp, עקומת המתיחה מתחילה לקבל קשר לא ליניארי. הדגימה נכנסת לשלב העיוות הראשוני, והעומס מוסר, והדגימה יכולה לחזור למצבה המקורי וליצור עיוות אלסטי.

ג. לאחר שהעומס עולה על Fe, העומס מוסר, חלק מהעיוות משוחזר, וחלק מהעיוות השיורי נשמר, וזה נקרא עיוות פלסטי. Fe נקרא גבול האלסטיות.

ד. כאשר העומס עולה עוד יותר, עקומת המתיחה מראה שן מסור. כאשר העומס אינו עולה או יורד, תופעת ההתארכות המתמשכת של הדגימה הניסיונית נקראת כניעה. לאחר הכניעה, הדגימה מתחילה לעבור דפורמציה פלסטית ברורה.

ה. לאחר כניעה, הדגימה מראה עלייה בעמידות לעיוות, התקשות בעבודה וחיזוק עיוות. כאשר העומס מגיע ל-Fb, אותו חלק של הדגימה מתכווץ בחדות. Fb הוא גבול החוזק.

ו. תופעת ההתכווצות מובילה לירידה בכושר הנשיאה של הדגימה. כאשר העומס מגיע ל-Fk, הדגימה נשברת. זה נקרא עומס שבר.

חוזק תפוקה

חוזק כניעה הוא ערך המאמץ המקסימלי שחומר מתכתי יכול לעמוד בו מתחילת העיוות הפלסטי ועד לשבר מלא כאשר הוא מופעל על ידי כוח חיצוני. ערך זה מסמן את הנקודה הקריטית שבה החומר עובר משלב העיוות האלסטי לשלב העיוות הפלסטי.

מִיוּן

חוזק כניעה עליון: מתייחס למאמץ המקסימלי של הדגימה לפני שהכוח יורד בפעם הראשונה כאשר מתרחשת כניעה.

חוזק כניעה נמוך יותר: מתייחס למאמץ המינימלי בשלב הכניעה כאשר מתעלמים מהאפקט החולף הראשוני. מכיוון שערך נקודת הכניעה התחתונה יציב יחסית, הוא משמש בדרך כלל כאינדיקטור לעמידות החומר, הנקראת נקודת כניעה או חוזק כניעה.

נוסחת חישוב

עבור חוזק כניעה עליון: R = F / Sₒ, כאשר F הוא הכוח המקסימלי לפני ירידת הכוח בפעם הראשונה בשלב הכניעה, ו-Sₒ הוא שטח החתך המקורי של הדגימה.

עבור חוזק כניעה נמוך יותר: R = F / Sₒ, כאשר F הוא הכוח המינימלי F תוך התעלמות מהאפקט החולף הראשוני, ו-Sₒ הוא שטח החתך המקורי של הדגימה.

יְחִידָה

יחידת המדידה של חוזק כניעה היא בדרך כלל MPa (מגה-פסקל) או N/mm² (ניוטון למילימטר רבוע).

דוּגמָה

קחו לדוגמה פלדה דלת פחמן, גבול הכניעה שלה הוא בדרך כלל 207MPa. כאשר היא נתונה לכוח חיצוני גדול מגבול זה, פלדה דלת פחמן תגרום לעיוות קבוע ולא ניתן יהיה לשחזר אותה; כאשר היא נתונה לכוח חיצוני קטן מגבול זה, פלדה דלת פחמן יכולה לחזור למצבה המקורי.

חוזק כניעה הוא אחד המדדים החשובים להערכת תכונות מכניות של חומרי מתכת. הוא משקף את יכולתם של חומרים להתנגד לעיוות פלסטי כאשר הם נתונים לכוחות חיצוניים.

חוזק מתיחה

חוזק מתיחה הוא יכולתו של חומר לעמוד בפני נזק תחת עומס מתיחה, המתבטא באופן ספציפי כערך המאמץ המרבי שהחומר יכול לעמוד בו במהלך תהליך המתיחה. כאשר מאמץ המתיחה על החומר עולה על חוזק המתיחה שלו, החומר יעבור עיוות פלסטי או שבר.

נוסחת חישוב

נוסחת החישוב לחוזק מתיחה (σt) היא:

σt = F / A

כאשר F הוא כוח המתיחה המקסימלי (ניוטון, N) שהדגימה יכולה לעמוד בו לפני שבירה, ו-A הוא שטח החתך המקורי של הדגימה (מילימטר מרובע, מ"מ²).

יְחִידָה

יחידת המדידה של חוזק מתיחה היא בדרך כלל MPa (מגה-פסקל) או N/mm² (ניוטון למילימטר רבוע). MPa אחד שווה ל-1,000,000 ניוטון למטר רבוע, שגם הוא שווה ל-1 N/mm².

גורמים משפיעים

חוזק מתיחה מושפע מגורמים רבים, כולל ההרכב הכימי, המיקרו-מבנה, תהליך טיפול בחום, שיטת העיבוד וכו'. לחומרים שונים יש חוזקי מתיחה שונים, ולכן ביישומים מעשיים, יש צורך לבחור חומרים מתאימים על סמך התכונות המכניות של החומרים.

יישום מעשי

חוזק מתיחה הוא פרמטר חשוב מאוד בתחום מדע והנדסת החומרים, והוא משמש לעתים קרובות להערכת התכונות המכניות של חומרים. מבחינת תכנון מבני, בחירת חומרים, הערכת בטיחות וכו', חוזק מתיחה הוא גורם שיש לקחת בחשבון. לדוגמה, בהנדסת בנייה, חוזק המתיחה של פלדה הוא גורם חשוב בקביעת האם היא יכולה לעמוד בעומסים; בתחום התעופה והחלל, חוזק המתיחה של חומרים קלים ובעלי חוזק גבוה הוא המפתח להבטחת בטיחותם של כלי טיס.

חוזק עייפות:

עייפות מתכת מתייחסת לתהליך שבו חומרים ורכיבים יוצרים בהדרגה נזק מצטבר קבוע מקומי במקום אחד או בכמה מקומות תחת לחץ מחזורי או עומס מחזורי, וסדקים או שברים פתאומיים שלמים מתרחשים לאחר מספר מסוים של מחזורים.

תכונות

פתאומיות בזמן: כשל עייפות מתכת מתרחש לעיתים קרובות פתאומי בפרק זמן קצר ללא סימנים ברורים.

מיקום במיקום: כשל עקב עייפות מתרחש בדרך כלל באזורים מקומיים שבהם מרוכז הלחץ.

רגישות לסביבה ופגמים: עייפות מתכת רגישה מאוד לסביבה ולפגמים זעירים בתוך החומר, אשר עלולים להאיץ את תהליך העייפות.

גורמים משפיעים

אמפליטודת מאמץ: גודל המאמץ משפיע ישירות על אורך חיי העייפות של המתכת.

גודל המאמץ הממוצע: ככל שהמאמץ הממוצע גדול יותר, כך אורך חיי העייפות של המתכת קצר יותר.

מספר מחזורים: ככל שהמתכת נמצאת תחת לחץ או מאמץ מחזורי יותר פעמים, כך הצטברות נזקי העייפות חמורה יותר.

אמצעי מניעה

אופטימיזציה של בחירת חומרים: בחירת חומרים בעלי גבולות עייפות גבוהים יותר.

הפחתת ריכוז מאמץ: הפחתת ריכוז מאמץ באמצעות תכנון מבני או שיטות עיבוד, כגון שימוש במעברים פינות מעוגלות, הגדלת ממדי חתך רוחב וכו'.

טיפול פני שטח: ליטוש, ריסוס וכו' על פני המתכת כדי להפחית פגמים במשטח ולשפר את חוזק העייפות.

בדיקה ותחזוקה: בדקו באופן קבוע רכיבי מתכת כדי לזהות ולתקן במהירות פגמים כגון סדקים; תחזוקה של חלקים הנוטים להתעייפות, כגון החלפת חלקים שחוקים וחיזוק חוליות חלשות.

עייפות מתכת היא מצב כשל נפוץ של מתכת, המאופיין בפתאומיות, מקומיות ורגישות לסביבה. משרעת המאמץ, גודל המאמץ הממוצע ומספר המחזורים הם הגורמים העיקריים המשפיעים על עייפות המתכת.

עקומת SN: מתארת ​​את אורך חיי העייפות של חומרים תחת רמות מאמץ שונות, כאשר S מייצג מאמץ ו-N מייצג את מספר מחזורי המאמץ.

נוסחת מקדם חוזק עייפות:

(Kf = Ka ≥ Kb ≥ Kc ≥ Kd ≥ Ke)

כאשר (Ka) הוא מקדם העומס, (Kb) הוא מקדם הגודל, (Kc) הוא מקדם הטמפרטורה, (Kd) הוא מקדם איכות פני השטח, ו-(Ke) הוא מקדם האמינות.

ביטוי מתמטי של עקומת SN:

(\sigma^m N = C)

כאשר (ρ) הוא המאמץ, N הוא מספר מחזורי המאמץ, ו-m ו-C הם קבועי החומר.

שלבי חישוב

קבע את קבועי החומר:

קבע את ערכי m ו-C באמצעות ניסויים או על ידי התייחסות לספרות רלוונטית.

קבע את גורם ריכוז המאמץ: יש לקחת בחשבון את הצורה והגודל בפועל של החלק, כמו גם את ריכוז המאמץ הנגרם על ידי פילטים, חריצי מפתח וכו', כדי לקבוע את גורם ריכוז המאמץ K. חשב את חוזק העייפות: בהתאם לעקומת SN וגורם ריכוז המאמץ, בשילוב עם אורך החיים המתוכנן ורמת מאמץ העבודה של החלק, חשב את חוזק העייפות.

2. גמישות:

פלסטיות מתייחסת לתכונה של חומר שכאשר הוא מופעל על ידי כוח חיצוני, הוא יוצר עיוות קבוע מבלי להישבר כאשר הכוח החיצוני חורג מגבול האלסטיות שלו. עיוות זה הוא בלתי הפיך, והחומר לא יחזור לצורתו המקורית גם אם הכוח החיצוני יוסר.

מדד הפלסטיות ונוסחת החישוב שלו

התארכות (δ)

הגדרה: התארכות היא האחוז מהדפורמציה הכוללת של קטע המדידה לאחר שהדגימה עוברת שבר מתיחה לאורך המדידה המקורי.

נוסחה: δ = (L1 – L0) / L0 × 100%

כאשר L0 הוא אורך המדידה המקורי של הדגימה;

L1 הוא אורך המדידה לאחר שבירת הדגימה.

צמצום מקטעי (Ψ)

הגדרה: הצמצום הסגמנטלי הוא אחוז הצמצום המקסימלי בשטח החתך בנקודת הצוואר לאחר שבירת הדגימה לשטח החתך המקורי.

נוסחה: Ψ = (F0 – F1) / F0 × 100%

כאשר F0 הוא שטח החתך המקורי של הדגימה;

F1 הוא שטח החתך בנקודת הצוואר לאחר שבירת הדגימה.

3. קשיות

קשיות מתכת היא מדד תכונות מכניות למדידת קשיות של חומרי מתכת. הוא מציין את היכולת לעמוד בפני עיוות בנפח המקומי על פני המתכת.

סיווג וייצוג של קשיות מתכת

לקשיות מתכת יש מגוון שיטות סיווג וייצוג בהתאם לשיטות בדיקה שונות. הן כוללות בעיקר את הדברים הבאים:

קשיות ברינל (HB):

היקף היישום: משמש בדרך כלל כאשר החומר רך יותר, כגון מתכות לא ברזליות, פלדה לפני טיפול בחום או לאחר חישול.

עקרון הבדיקה: עם עומס בדיקה בגודל מסוים, כדור פלדה מוקשה או כדור קרביד בקוטר מסוים נלחץ לתוך פני המתכת לבדיקה, והעומס פורק לאחר זמן מוגדר, ונמדד קוטר השקע על פני השטח לבדיקה.

נוסחת חישוב: ערך קשיות ברינל הוא המנה המתקבלת על ידי חלוקת העומס בשטח הפנים הכדורי של השקע.

קשיות רוקוול (HR):

היקף היישום: משמש בדרך כלל לחומרים בעלי קשיות גבוהה יותר, כגון קשיות לאחר טיפול בחום.

עקרון הבדיקה: דומה לקשיות ברינל, אך באמצעות גלאים שונים (יהלום) ושיטות חישוב שונות.

סוגים: בהתאם ליישום, ישנם HRC (לחומרים בעלי קשיות גבוהה), HRA, HRB וסוגים נוספים.

קשיות ויקרס (HV):

היקף יישום: מתאים לניתוח במיקרוסקופ.

עקרון הבדיקה: לחץ על פני החומר בעומס של פחות מ-120 ק"ג ועל חרוט יהלום מרובע עם זווית קודקוד של 136 מעלות, וחלק את שטח הפנים של בור החריצה של החומר בערך העומס כדי לקבל את ערך הקשיות של ויקרס.

קשיות ליב (HL):

מאפיינים: בודק קשיות נייד, קל למדידה.

עקרון הבדיקה: השתמש בקפיצה שנוצרת על ידי ראש כדור הפגיעה לאחר הפגיעה במשטח הקשיות, וחשב את הקשיות לפי היחס בין מהירות הריבאונד של האגרוף במרחק של 1 מ"מ ממשטח הדגימה למהירות הפגיעה.